Continuidad uniforme

En análisis matemático una función f(x) se dice que es uniformemente continua si pequeños cambios en el valor de x producen pequeños cambios en el valor de la función (continuidad) y el tamaño de los cambios en f(x) depende solo del tamaño de los cambios en x pero no del valor de x (uniforme).

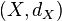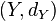Dados dos espacios métricos  y , y  entonces una función 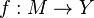 se llama uniformemente continua en M si para cualquier número real  existe  tal que 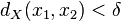, se tiene que  para todo .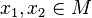

Una función 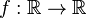 es uniformemente continua en un intervalo  si para todo  existe algún  tal que para todo  se cumple que si , entonces 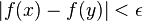.¹

A diferencia de en la continuidad, donde el valor de  depende del punto x, en las funciones uniformemente continuas, no.

Ejemplo:

• La función 1/x con x>0 es continua pero no uniformemente continua
• La función x es uniformemente continua en el intevalo [0,1].
• Todo polinomio  cuyo grado sea mayor o igual que uno es uniformemente continuo en un intervalo cerrado.

Resultados

• De la definción se deduce que toda función uniformemente continua es continua. Lo contrario (toda función continua es uniformemente continua) no siempre es cierto. Ejemplo: Si 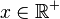 y 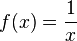.  es continua y no es uniformemente continua. Sin embargo, se verifica que:

Si M es un espacio métrico compacto e Y un espacio métrico, entonces toda función continua f : M → Y es uniformemente continua. En particular, toda función continua sobre un intervalo cerrado y acotado es uniformemente continua en dicho intervalo (Teorema de Heine-Cantor).

• Si (x_n) es una sucesión de Cauchy contenida en el dominio de f (no necesariamente convergente) y f es una función uniformemente continua, entonces (f(x_n)) también es una sucesión de Cauchy.
• Toda función Lipschitz continua es uniformemente continua.