Una sucesión matemática es un conjunto ordenado de objetos matemáticos, generalmente números.
Cada uno de ellos es denominado término (también elemento o miembro) de la sucesión y al número de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesión. No debe confundirse con una serie matemática, que es la suma de los términos de una sucesión.
Cada uno de ellos es denominado término (también elemento o miembro) de la sucesión y al número de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesión. No debe confundirse con una serie matemática, que es la suma de los términos de una sucesión.
A diferencia de un conjunto, el orden en que aparecen los términos sí es relevante y un mismo término puede aparecer en más de una posición. De manera formal, una sucesión puede definirse como una función sobre el conjunto de los números naturales (o un subconjunto del mismo) y es por tanto una función discreta.
- Ejemplo
La sucesión (A, B, C) es una sucesión de letras que difiere de la sucesión (C, A, B). En este caso se habla de sucesiones finitas (de longitud igual a 3). Un ejemplo de sucesión infinita sería la sucesión de números positivos pares: 2, 4, 6, 8, ...
En ocasiones se identifica a las sucesiones finitas con palabras sobre un conjunto. Puede considerarse también el caso de una sucesión vacía (sin elementos), pero este caso puede excluirse dependiendo del contexto.
Definición formal
Una sucesión finita  (de longitud r) con elementos pertenecientes a un conjunto S, se define como una función
(de longitud r) con elementos pertenecientes a un conjunto S, se define como una función
 (de longitud r) con elementos pertenecientes a un conjunto S, se define como una función
(de longitud r) con elementos pertenecientes a un conjunto S, se define como una función.
y en este caso el elemento  corresponde a
corresponde a  .
.
 corresponde a
corresponde a  .
.
Por ejemplo, la sucesión finita, (de longitud 4) de números primos menores que 10:
corresponde a la función  (donde
(donde  es el conjunto de números primos) definida por:
es el conjunto de números primos) definida por:
 (donde
(donde  es el conjunto de números primos) definida por:
es el conjunto de números primos) definida por:.
Una sucesión infinita  con elementos pertenecientes a un conjunto S, se define como una función
con elementos pertenecientes a un conjunto S, se define como una función
 con elementos pertenecientes a un conjunto S, se define como una función
con elementos pertenecientes a un conjunto S, se define como una función.
en donde, de forma análoga,  corresponde a
corresponde a  .
.
 corresponde a
corresponde a  .
.Notación
Notaremos por  a una sucesión, donde x la identifica como distinta de otra digamos
a una sucesión, donde x la identifica como distinta de otra digamos  .
.
 a una sucesión, donde x la identifica como distinta de otra digamos
a una sucesión, donde x la identifica como distinta de otra digamos  .
.
La notación es permisiva en cuanto a su modificación si realmente es necesario.
Definición de término general
Llamaremos término general de una sucesión a  ,donde el subíndice
,donde el subíndice  indica el lugar que ocupa en dicha sucesión.
indica el lugar que ocupa en dicha sucesión.
 ,donde el subíndice
,donde el subíndice  indica el lugar que ocupa en dicha sucesión.
indica el lugar que ocupa en dicha sucesión.Definición de parcial
Llamaremos parcial de  a una sucesión
a una sucesión  donde
donde 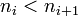 .
.
 a una sucesión
a una sucesión  donde
donde 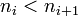 .
.
Notación
Existen diferentes notaciones y nociones de sucesión en matemáticas, dependiendo del área de estudio, algunas de las cuales (como por ejemplo sucesión exacta) no quedan comprendidas en la notación que se introduce a continuación.
Se puede usar la notación  para indicar una sucesión, en donde
para indicar una sucesión, en donde  hace referencia al elemento de la sucesión en la posición n.
hace referencia al elemento de la sucesión en la posición n.
 para indicar una sucesión, en donde
para indicar una sucesión, en donde  hace referencia al elemento de la sucesión en la posición n.
hace referencia al elemento de la sucesión en la posición n.
Ejemplo. Retomando el ejemplo de los números positivos pares, si denotamos dicha sucesión por 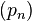 :
:
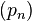 :
:
entonces
.
En el caso de que los elementos de la sucesión queden determinados por una regla, se puede especificar la sucesión haciendo referencia a la fórmula de un término arbitrario. Ejemplo. La sucesión anterior 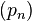 puede especificarse mediante la fórmula
puede especificarse mediante la fórmula 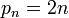 .
.
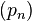 puede especificarse mediante la fórmula
puede especificarse mediante la fórmula 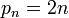 .
.
No es infrecuente encontrar sucesiones en donde los subíndices denotando posiciones inician desde cero, en vez desde uno, particularmente en matemática discreta o en ciencias de la computación. También se puede usar una variable distinta a n para denotar el término general, cuando así convenga para evitar confusión con otras variables.
En la literatura es posible encontrar una gran variedad de notaciones alternativas. Por ejemplo, uso de llaves en vez de paréntesis, o indicaciones de los límitesmediante variantes de super y subíndices, a continuación se muestran algunos pocos ejemplos:
Una sucesión numérica se formaliza como una aplicación de los números naturales sobre otro conjunto numerico, así por ejemplo:
Una sucesión de N sobre N, como la sucesión de Fibonacci.
Si la sucesión numérica se formaliza como una aplicación de los números naturales en los números reales, es decir :
En cualquier caso se denota simplemente como  o, si se da por entendido que los subíndices son enteros, también se denota como
o, si se da por entendido que los subíndices son enteros, también se denota como  .
.
 o, si se da por entendido que los subíndices son enteros, también se denota como
o, si se da por entendido que los subíndices son enteros, también se denota como  .
.
El nombre que recibe la sucesión también puede hacer referencia a los valores que toma sobre los reales; así, si la imagen de  fuesen los racionales, es decir fracciones enteras del tipo
fuesen los racionales, es decir fracciones enteras del tipo  , se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos,trascendentes, ...
, se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos,trascendentes, ...
 fuesen los racionales, es decir fracciones enteras del tipo
fuesen los racionales, es decir fracciones enteras del tipo  , se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos,trascendentes, ...
, se puede llamar sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos,trascendentes, ...
Puede ser creciente o decreciente. Las hay en progresión aritmética o en progresión geométrica, la diferencia básica es que en la sucesión aritmética la razón de cambio entre un miembro y otro es la suma o resta de la misma razón, y en la sucesión geométrica el siguiente número de la sucesión se logra por multiplicar o dividir la razón de cambio. En cualquier caso la razón de cambio es constante y no puede variar, a menos que el cambio de la razón también corresponda a una sucesión, lo que supone tener una sucesión dentro de otra sucesión.
El término general de la sucesión queda definido de forma implícita si su valor depende de sus predecesores. En general, dados previamente los valores de 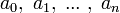 , podemos definir el término general de forma inductiva como
, podemos definir el término general de forma inductiva como  como por ejemplo con la ecuación en recurrencias
como por ejemplo con la ecuación en recurrencias 
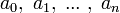 , podemos definir el término general de forma inductiva como
, podemos definir el término general de forma inductiva como  como por ejemplo con la ecuación en recurrencias
como por ejemplo con la ecuación en recurrencias 
Sucesión finita
Se dice que una sucesión es finita si determinamos su último término, por ejemplo el n-ésimo:
- Genéricamente:
 , donde
, donde  sería el término general si hiciese falta.
sería el término general si hiciese falta.
- ejemplo: 100, 99, 98, ... , 1, 0
Sucesión constante
Se dice que una sucesión es constante si todos los términos valen un mismo valor, , es decir, un mismo número real cualquiera, ejemplo:
, es decir, un mismo número real cualquiera, ejemplo:- Genéricamente

- ejemplo: si
 queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1 - Sucesiones monótonas
- Una sucesión monótona es una sucesión creciente o decreciente
Sucesión creciente
Si se impone al término general de una sucesión numérica la condición que , es decir, que el siguiente término,
, es decir, que el siguiente término,  , siempre sea mayor estricto que su predecesor,
, siempre sea mayor estricto que su predecesor,  , se llaman sucesiones estrictamente crecientes:
, se llaman sucesiones estrictamente crecientes:- Para naturales: 1, 2, 3, 4, 5, 6, ...
- Para enteros: -10, -9, -8, -7, -6, ...
- Para reales:
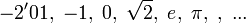 .
.
Si se impone , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.Sucesión decreciente
Al igual que las crecientes tenemos, según el término general, que:- si
 es estrictamente decreciente.
es estrictamente decreciente. - si
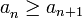 entonces la sucesión es decreciente.
entonces la sucesión es decreciente.
Sucesión alternada
Intuitivamente se llama sucesión alternada cuando alterna valores de signo opuesto, como que nos genera la sucesión: a0=1, -1, 1, -1, 1, -1, ... utilizada por las series llamadas series alternadas.
que nos genera la sucesión: a0=1, -1, 1, -1, 1, -1, ... utilizada por las series llamadas series alternadas.Sucesiones Acotadas
Se pueden dar tres formas de sucesión acotada:- Una sucesión {an} estará acotada superiormente en el caso que exista un número real M que limite de la siguiente forma la secuencia: {an} ≤ M.
- Por otro lado, la sucesión estará acotada inferiormente cuando un número real N la limite de la forma contraria a la anterior: {an} ≥ N.
- Finalmente, en caso de que se den ambas opciones {an} será una sucesión acotada.
Sucesiones Convergentes
Una sucesión , converge a
, converge a  o tiene por límite
o tiene por límite  (cuando
(cuando  ), y se escribe,cuando,
), y se escribe,cuando,Propiedades
Unicidad del límite de una sucesión
Si una sucesión converge, entonces el
converge, entonces el  es únicoDemostraciónSean
es únicoDemostraciónSean de forma que,Entonces se cumplen estos dos asertos,Primero,Segundo,luego para
de forma que,Entonces se cumplen estos dos asertos,Primero,Segundo,luego para ,Como
,Como fue elegido de forma arbitraria entonces
fue elegido de forma arbitraria entonces 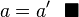
Relación entre el concepto de sucesión acotada y el de sucesión convergente
Si una sucesión es convergente, entonces está acotada.DemostraciónUna sucesión
es convergente, entonces está acotada.DemostraciónUna sucesión es convergente cuando,luego en particular, por ejemplo, para
es convergente cuando,luego en particular, por ejemplo, para (podríamos haber tomado cualquier otro
(podríamos haber tomado cualquier otro  ) se verifica que,Ahora bien,luego hemos concluido que
) se verifica que,Ahora bien,luego hemos concluido que se verifica que,Se debe encontrar un
se verifica que,Se debe encontrar un de forma que
de forma que  sea
sea  . Como a partir del índice
. Como a partir del índice 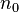 se cumple, sumando a
se cumple, sumando a  todos los elementos que van por detrás de
todos los elementos que van por detrás de 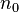 hasta el elemento 1 de la sucesión ya tendríamos el
hasta el elemento 1 de la sucesión ya tendríamos el  buscado.Entonces si,se tiene que,
buscado.Entonces si,se tiene que,
- Genéricamente


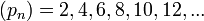

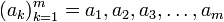

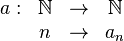




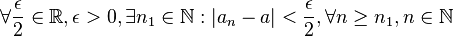
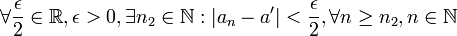

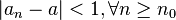
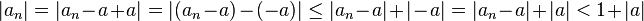
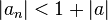


Acá les dejo parte de la unidad II
ResponderEliminarMuy buena la información sobre sucesiones
EliminarEs importante saber que no se debe confundir sucesiones con una serie matemática
EliminarLos que tienen las copias del libro de Zuleima de Barragan, ahi también hay contenido de Sucesiones en el Capitulo IV pág. 181. Hay encontraran informacion Teoremas y como se demuestran
ResponderEliminarEn análisis matemático, una sucesión de números reales se define como un conjunto A no vacío. Una sucesión de elementos de A es una aplicación del conjunto N de los números naturales en A. En particular, una sucesión de números reales es una aplicación del conjunto N de los números naturales en el conjunto R de los números reales.
ResponderEliminar