En el análisis matemático, el teorema de Heine-Borel (también llamado teorema de Heine-Borel-Lebesgue-Bolzano-Weierstraß o incluso teorema de Borel-Lebesgue) es uno que establece condiciones para que un subconjunto de 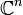 o de
o de  sea compacto. Cuando se refiere al caso particular de la recta real recibe el nombre de Teorema de Heine-Borel. En el resto de los casos, es frecuente llamarlo Teorema de Borel-Lebesgue.
sea compacto. Cuando se refiere al caso particular de la recta real recibe el nombre de Teorema de Heine-Borel. En el resto de los casos, es frecuente llamarlo Teorema de Borel-Lebesgue.
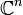 o de
o de  sea compacto. Cuando se refiere al caso particular de la recta real recibe el nombre de Teorema de Heine-Borel. En el resto de los casos, es frecuente llamarlo Teorema de Borel-Lebesgue.
sea compacto. Cuando se refiere al caso particular de la recta real recibe el nombre de Teorema de Heine-Borel. En el resto de los casos, es frecuente llamarlo Teorema de Borel-Lebesgue.El teorema se enuncia de la siguiente manera:
Si un conjunto
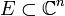 tiene alguna de las siguientes propiedades, entonces tiene las otras dos:
tiene alguna de las siguientes propiedades, entonces tiene las otras dos: es cerrado y acotado.
es cerrado y acotado. es compacto.
es compacto.- Todo subconjunto infinito de
 tiene un punto de acumulación en la frontera de
tiene un punto de acumulación en la frontera de  .
.
Teoremas preliminares
|
Sea  un conjunto cerrado y
un conjunto cerrado y  un conjunto compacto tales que
un conjunto compacto tales que 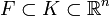 .
.
 un conjunto cerrado y
un conjunto cerrado y  un conjunto compacto tales que
un conjunto compacto tales que 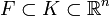 .
.
Sea 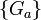 una cubierta abierta de
una cubierta abierta de  , entonces
, entonces 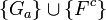 es una cubierta abierta de
es una cubierta abierta de  (podemos agregar
(podemos agregar 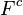 ya que es abierto). Como
ya que es abierto). Como  es compacto entonces
es compacto entonces  tiene un refinamiento finito que también cubre a
tiene un refinamiento finito que también cubre a  . Podemos quitar a
. Podemos quitar a 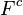 y sigue cubriendo a
y sigue cubriendo a  . Así obtenemos un refinamiento finito de cualquier cubierta abierta de
. Así obtenemos un refinamiento finito de cualquier cubierta abierta de 
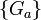 una cubierta abierta de
una cubierta abierta de  , entonces
, entonces 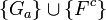 es una cubierta abierta de
es una cubierta abierta de  (podemos agregar
(podemos agregar 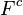 ya que es abierto). Como
ya que es abierto). Como  es compacto entonces
es compacto entonces  tiene un refinamiento finito que también cubre a
tiene un refinamiento finito que también cubre a  . Podemos quitar a
. Podemos quitar a 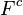 y sigue cubriendo a
y sigue cubriendo a  . Así obtenemos un refinamiento finito de cualquier cubierta abierta de
. Así obtenemos un refinamiento finito de cualquier cubierta abierta de 
Si  no tuviera puntos de acumulación en no tuviera puntos de acumulación en  entonces entonces 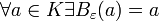 donde donde 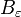 es una epsilon-vecindad y es una epsilon-vecindad y  . Es claro que el conjunto de estas vecindades forman una cubierta par . Es claro que el conjunto de estas vecindades forman una cubierta par  pero no tiene un refinamiento finito, lo mismo cumpliría para pero no tiene un refinamiento finito, lo mismo cumpliría para  que contradiría la definición de que que contradiría la definición de que  es compacto. es compacto.Toda k-celda es compacta
Sea
 una k-celda que consiste de todos los puntos x una k-celda que consiste de todos los puntos x tal que tal que 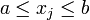 y y  . Sea . Sea 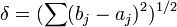 entonces si entonces si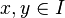  . Sea . Sea 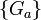 una cubierta arbitraria de una cubierta arbitraria de  y supongamos que y supongamos que  no se puede cubrir con una cantidad finita de no se puede cubrir con una cantidad finita de 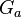 's. 's.
Tomemos
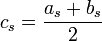 entonces los intervalos entonces los intervalos ![[a_s,c_s] [c_s,b_s]](http://upload.wikimedia.org/math/e/0/3/e0376193991ba406de527dff3fcbc224.png) determinan determinan 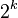 celdas celdas 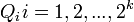 . Entonces por lo menos un . Entonces por lo menos un  no se puede cubrir con una cantidad finita de no se puede cubrir con una cantidad finita de 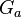 's. Lo llamaremos 's. Lo llamaremos  y así obtenemos una sucesión y así obtenemos una sucesión 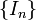 tal que: tal que:
Digamos que
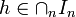 , como , como 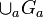 cubre a cubre a  entonces entonces 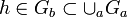 . Como . Como 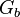 es abierto es abierto 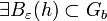 . Si tomamos n suficientemente grande tal que . Si tomamos n suficientemente grande tal que  tenemos que este tenemos que este  lo cual contradice la suposición de que no se puede cubrir con una cantidad finita de lo cual contradice la suposición de que no se puede cubrir con una cantidad finita de 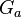 's. 's.Demostración del teorema de Heine-Borel
Si cumple 1) entonces
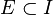 para alguna k-celda para alguna k-celda  , y 1) implicaría 2) por los teoremas 1 y 3 anteriores.Si se cumple 2), entonces se cumple 3) por el teorema 2 anterior.Ahora falta demostrar que si cumple 3), entonces cumple 1): Si , y 1) implicaría 2) por los teoremas 1 y 3 anteriores.Si se cumple 2), entonces se cumple 3) por el teorema 2 anterior.Ahora falta demostrar que si cumple 3), entonces cumple 1): Si  no es conexo entonces contiene un conjunto { no es conexo entonces contiene un conjunto { } tal que } tal que 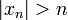 entonces el subconjunto { entonces el subconjunto { } es finito y tiene un límite en } es finito y tiene un límite en  , lo cual contradice 3). Si , lo cual contradice 3). Si  no es abierto entonces existe un elemento no es abierto entonces existe un elemento 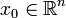 que es un punto de acumulación de que es un punto de acumulación de  pero no está en pero no está en  . Para . Para 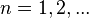 existen existen 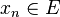 tales que tales que 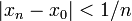 , entonces el conjunto { , entonces el conjunto { } es infinito y tiene límite contenido en él mismo, lo cual contradice 3). } es infinito y tiene límite contenido en él mismo, lo cual contradice 3). |

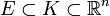 , donde
, donde 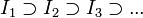 .
.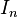 no se puede cubrir con una cantidad finita de
no se puede cubrir con una cantidad finita de  entonces
entonces 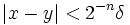 .
.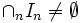
El teorema de Heine-Borel también llamado teorema de Borel-Lebesgue en el análisis matemático establece: Un subconjunto de es cerrado y acotado si y solo si es compacto, esto es si admite un recubrimiento infinito admite también un recubrimiento finito, en el caso particular aplicado a la recta real recibe propiamente el nombre de Teorema de Heine-Borel fuera de este caso es frecuente llamarlo Teorema de Borel-Lebesgue.
ResponderEliminarMalditos
ResponderEliminar